Calculate Heat Flux Through A Sheet Of Steel

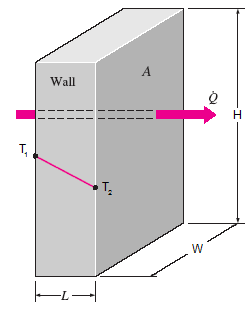
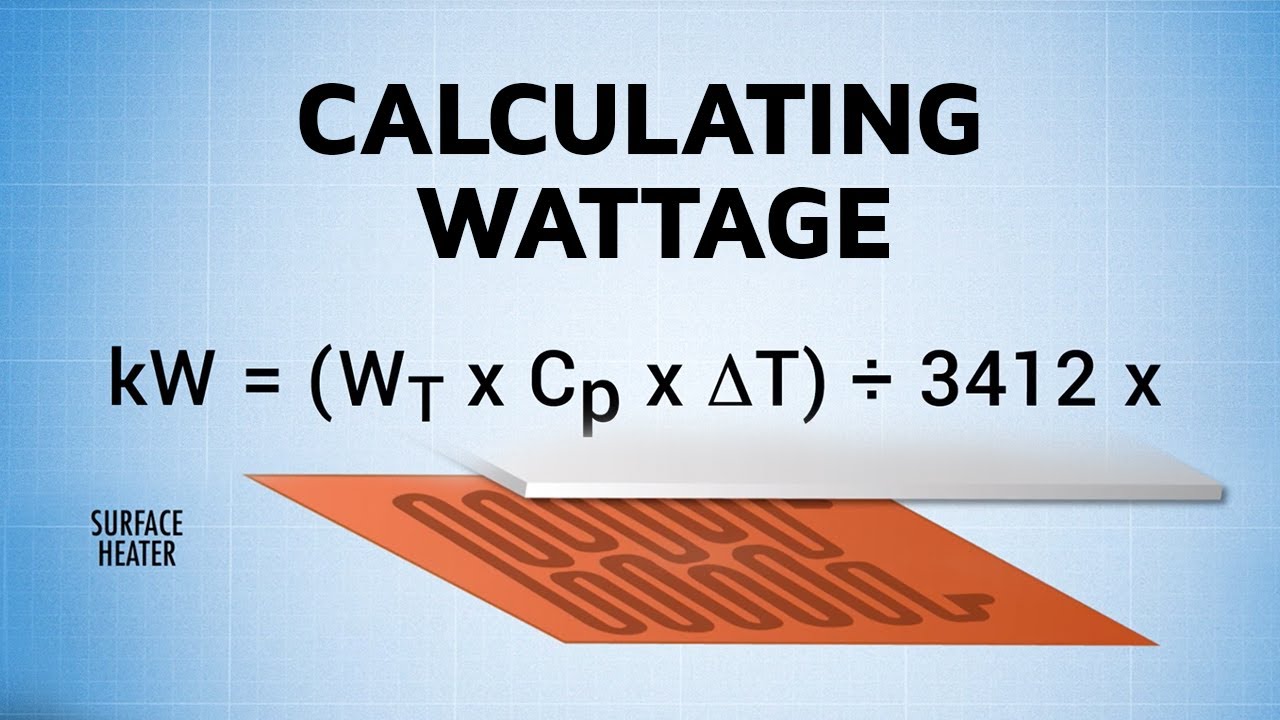Calculate the heat flux through a sheet of steel 10mm 0 39 in thick if the temperatures at the two faces are 300 and 100 c 572 and 212 f.

Calculate heat flux through a sheet of steel.

Assume steady state heat flow. What is the heat loss per hour if the area of the sheet is 0 25 m2 2 7 ft2. The heat flux can be given as. C what will be the heat loss per hour if soda lime glass is used instead of steel.

Thermal conductivity of material w mk or. B what is the heat loss per hour if the area of the sheet is 0 25 m 2 2 7 ft 2. Assume steady state heat flow. Calculate overall heat transfer coefficient.

Thermal conductivity k is the quantity of heat transmitted due to an unit temperature gradient in unit time under steady conditions in a direction normal to a surface of the unit area. Steel thickness x 10 mm 10 10 3 m temperature difference between two faces δ t 300 100 200 c 0 calculation. C what will be the heat loss per hour if sodalime glass instead of steel is used. The thermal conductivity of the stainless steel is 19 w m k and the thermal conductivity of the insulation board is 0 7 w m k.

A calculate the heat flux through a sheet of steel 10 mm 0 39 in thick if the temperatures at the two faces are 300 c and 100 c 572 f and 212 f. B what is the heat loss per hour if the area of the sheet is 0 25 m. D calculate the heat loss per hour. A calculate the heat flux through a sheet of steel 10 mm 0 39 in thick if the temperatures at the two faces are 300 and 100 c 572 and 212 f.

Assume steady state heat flow. Calculate the heat loss per hour if. Cross sectional area m 2. Assume steady state heat flow.

Thermal conductivity k is used in the fourier s equation. Assume steady state heat flow. A calculate the heat flux through a sheet of steel 10 mm 0 39 in thick if the temperatures at the two faces are 300 and 100 c 572 and 212 f. A calculate the heat flux through a sheet of steel 10 mm 0 39 in thick if the temperatures at the two faces are 300 and 100 c 572 and 212 f.

Steady state heat flow solution. The conductive heat transport through the layered wall can be calculated as q 800 k 350 k 1 m2 0 012 m 19 w m k 0 05 m 0 7 w m k 6245 w. Input the cross sectional area m 2 add your materials thickness m enter the hot side temperature c enter the cold side temperature c click calculate solve for conduction heat transfer. Calculate conductive heat transfer.